September 29th, 2014 | 6 Comments
Some time ago I introduced already a waterfall plot, which I named a pseudo-3D-plot. In the meantime, I have been asked several times for a colored version of such a plot. In this post we will revisit the waterfall plot and add some color to it.
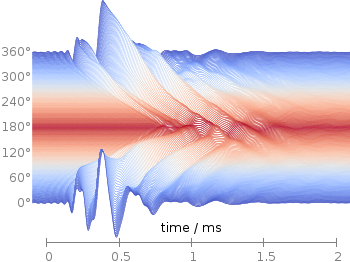
Fig. 1 Waterfall plot of head related impulse responses. (code to produce this figure, color palette, data)
In Fig. 1 the same head related impulse responses we animated already are displayed in a slightly different way. They describe the transmission of sound from a source to a receiver placed in the ear canal dependent on the position of the source. Here, we show the responses for all incident angles of the sound at once. At 0° the source was placed at the same side of the head as the receiver.
The color is added by applying the Moreland color palette, which we discussed earlier. The palette is defined in an extra file and loaded, this enables easy reuse of defined palettes. In the plotting command the palette is enabled with the lc palette command, that tells gnuplot to use the palette as line color depending on the value of the third column, which is given by color(angle).
load 'moreland.pal'
set style fill solid 0.0 border
limit360(x) = x180?360-x:x
amplitude_scaling = 200
plot for [angle=360:0:-2] 'head_related_impulse_responses.txt' \
u 1:(amplitude_scaling*column(limit360(angle)+1)+angle):(color(angle)) \
w filledcu y1=-360 lc palette lw 0.5
To achieve the waterfall plot, we start with the largest angle of 360° and loop through all angles until we reach 0°. The column command gives us the corresponding column the data is stored in the data file, amplitude_scaling modifies the amplitude of the single responses, and +angle shifts the data of the single responses along the y-axis to achieve the waterfall.
Even though the changing color in the waterfall plot looks nice you should always think if it really adds some additional information to the plot. If not, a single color should be used. In the following the same plot is repeated, but only with black lines and different angle resolutions which also have a big influence on the final appearance of the plot.
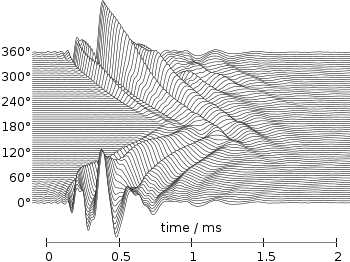
Fig. 2 Waterfall plot of head related impulse responses with a resolution of 5°. (code to produce this figure, data)
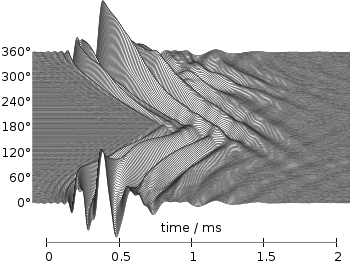
Fig. 3 Waterfall plot of head related impulse responses with a resolution of 2°. (code to produce this figure, data)
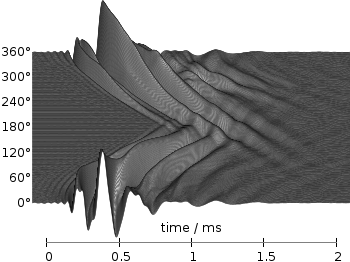
Fig. 4 Waterfall plot of head related impulse responses with a resolution of 1°. (code to produce this figure, data)