pm3d « Gnuplotting

January 31st, 2014 | 3 Comments

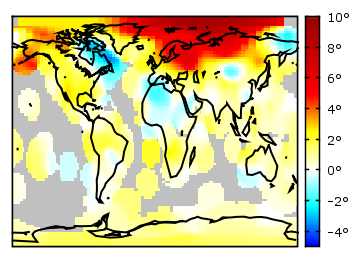
And another plot of the world. This time we are dealing with the raster data from Natural Earth. This data is normally available as tif-files. To use them in gnuplot we have to convert them first, then we can create a plot as shown in Fig. 1.

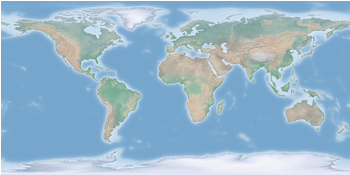
Fig. 1 Cross-blended hypsometric tint plot of the world. (code to produce this figure, data)

The conversion is done by the convert_natural_earth script. There the tif-file is first scaled down to the desired resolution using imagemagick. Afterwards it is converted to a text file and reordered for the splot command of gnuplot. The text file includes the longitude, latitude and three rgb color values.
You have to invoke the script in the following way.

$ ./convert_natural_earth $RES $FILE

where $RES is the desired resolution in pixel of your gnuplot plot and $FILE the input tif-file.
After finished we can plot the resulting text file simply by

set datafile separator ','
set size ratio -1
plot 'HYP_50M_SR_W_350px.txt' w rgbimage

which results in Fig. 1.

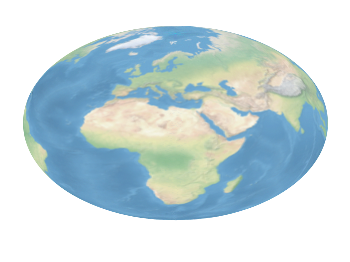
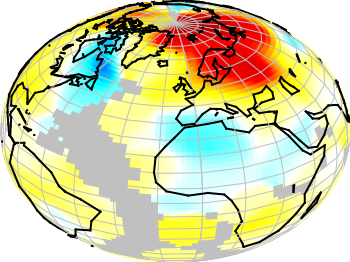
Fig. 2 Natural Earth II shaded relief and water plot of the world. (code to produce this figure, data)

The image can also be projected on a 3D figure of the world as shown in Fig. 2. To achieve this the three rgb values have to be summarized in one value and the rgb variable line color option has to be chosen together with pm3d.

rgb(r,g,b) = 65536 * int(r) + 256 * int(g) + int(b)
set mapping spherical
set angles degrees
splot 'NE2_50M_SR_W_700px.txt' u 1:2:(1):(rgb($3,$4,$5)) w pm3d lc rgb variable

Tags: angles, datafile, pm3d, rgb, rgbimage, sphere, splot, tif, variable

August 22nd, 2013 | 30 Comments

On the PGF plots page I found a nice example of visualizing data with cubes. Here we will recreate the same with gnuplot as you can see in Fig. 1.

Fig. 1 Cubes with different colors. (code to produce this figure, cube function, data)

We need basically two things in order to achieve it. First we have to plot a single cube with gnuplot. This is not as straight forward as you may think. We have to define a data file for it and plot it with the pm3d style which will result in Fig. 2.

# single cube
0 0 0
0 0 1
0 1 1
0 1 0
0 0 0

1 0 0
1 0 1
1 1 1
1 1 0
1 0 0

0 0 0
1 0 0
1 1 0
0 1 0
0 0 0

0 0 1
1 0 1
1 1 1
0 1 1
0 0 1

set cbrange [0.9:1]
set palette defined (1 '#ce4c7d')
set style line 1 lc rgb '#b90046' lt 1 lw 0.5
set pm3d depthorder hidden3d
set pm3d implicit
unset hidden3d
splot 'cube.txt' u 1:2:3:(1) w l ls 1

The use of the fourth (1) column for the splot command ensures that the cube gets the same color on every side. Only the edges are highlighted by a slighty different color given by the line style.

Fig. 2 A single cube. (code to produce this figure, data)

In a second step we reuse the code from the Object placement using a data file entry in order to plot cubes at different positions with different colors. To get the different colors and positions we replace the cube.txt file with a cube function that returns the values for the desired position and color.

add_cube(x,y,z,c) = sprintf('cube(%f,%f,%f,%i) w l ls %i,',x,y,z,c,c)
CMD = ''
stats 'cube_positions.txt' u 1:(CMD = CMD.add_cube($1,$2,$3,$4)) nooutput
CMD = 'splot '.CMD.'1/0 w l ls 2'
eval(CMD)

Tags: cube, eval, hidden3d, implicit, pm3d, splot, sprintf, stats

March 12th, 2013 | 12 Comments

We discussed already the plotting of heat maps at more than one occasions. Here we will add the possibility to interpolate the data in a heat map figure.

Fig. 1 A simple heat map (code to produce this figure, data)

Suppose we have the following data matrix, stored in heat_map_data.txt.

6 5 4 3 1 0
3 2 2 0 0 1
0 0 0 0 1 0
0 0 0 0 2 3
0 0 1 2 4 3
0 1 2 3 4 5

The normal way of plotting them would be with

plot 'heat_map_data.txt' matrix with image

But to be able to interpolate the data we have to use splot and pm3d instead.

set pm3d map
splot 'heat_map_data.txt' matrix

In Fig. 1 the result of plotting the data just with splot, without interpolation is shown. Note, that the result differs already from the plot command. The plot command would have created six points, whereas the splot command comes up with only five different regions for every axis.

Fig. 2 A heat map interpolated to use twice as much points on every axis (code to produce this figure, data)

Now if we want to double the number of visible points, we can tell pm3d easily to interpolate the data by the interpolate command.

set pm3d interpolate 2,2

The two numbers 2,2 are the number of additional points along the x- and y-axis.
The resulting plot can be found in Fig. 2.

Fig. 3 A heat map interpolated with an optimal number of points (code to produce this figure, data)

In addition to explicitly setting the number of points we can tell gnuplot to choose the correct number of interpolation points by itself, by setting them to 0.

set pm3d interpolate 0,0

Now gnuplot decides by itself how to interpolate, which leads to the result in Fig. 3.

Tags: colormap, image, interpolate, matrix, pm3d, splot

July 29th, 2011 | 5 Comments

In one post we have used the parametric plot option to plot the world. Here we want to add some temperature data as a heat map to the world plots. The data show the temperature anomalies of the year 2005 in comparison to the baseline 1951-1980 and is part of the GISTEMP data set.

Fig. 1 A 2D heat map of the temperature anomalies in 2005 to the baseline 1951-1980 (code to produce this figure, temperature data, world data)

The first problem you face, if you want to create a heat map, is that the data has to be in a specific format shown in the Gnuplot example page for heat maps. Therefore we first arrange the data and end up with this temperature anomalies file. Unknown data points are given by 9999.0.

In order to plot this data to the 2D world map we have to add a reasonable cbrange and a color palette and the plot command for the map:

set cbrange [-5:10]
set palette defined (0 "blue",17 "#00ffff",33 "white",50 "yellow",\
    66 "red",100 "#990000",101 "grey")
plot 'temperature.dat' u 2:1:3 w image, \
     'world.dat' with lines linestyle 1

The trick with the wide range from 0 to 101 for the color bar is chosen in order to use grey for the undefined values (9999.0) without seeing the grey color in the color bar. The result is shown in Fig. 1.

Fig. 2 A 3D heat map of the temperature anomalies in 2005 to the baseline 1951-1980 (code to produce this figure, temperature data, world data)

The same data can easily be applied to the 3D plot of the world. We have to add front to the hidden3d command in order to make the black world lines visible. In addition the radius must be given explicitly as third column to the plot command for the temperature data.

set hidden3d front
splot 'temperature.dat' u 2:1:(1):3 w pm3d, \
      r*cos(v)*cos(u),r*cos(v)*sin(u),r*sin(v) w l ls 2, \
      'world.dat' u 1:2:(1) w l ls 1

The result is shown in Fig. 2.

Tags: data, hidden3d, parametric, pm3d, sphere

June 7th, 2011 | 6 Comments

A Klein bottle is a non-orientable surface, which has no defined left and right, as stated on Wikipedia. There we can also find a Gnuplot plot of the bottle, which we want to fine-tune a little bit in order to reach the result in Fig. 1.

Fig. 1 Klein bottle (code to produce this figure)

In order to reach Fig. 1 we start with the definition of the parametric functions given in Wikipedia and do a simple pm3d plot with them.

set parametric
x(u,v)= v<2*pi ? (2.5-1.5*cos(v))*cos(u) : \
        v<3*pi ? -2+(2+cos(u))*cos(v)    : \
                 -2+2*cos(v)-cos(u)
y(u,v)= v<2*pi ? (2.5-1.5*cos(v))*sin(u) : \
                sin(u)
z(u,v)= v<pi   ? -2.5*sin(v)             : \
        v<2*pi ? 3*v-3*pi                : \
        v<3*pi ? (2+cos(u))*sin(v)+3*pi  : \
                 -3*v+12*pi
splot x(u,v),y(u,v),-z(u,v) w pm3d

The result is shown in Fig. 2.

Fig. 2 Klein bottle plotted only with pm3d (code to produce this figure)

Now we add some lines to the surface and hide parts, which are not visible in 3d.

set pm3d depthorder hidden3d 1
set hidden3d

Here the depthorder option takes care of the right positioning of the bottleneck going back into the bottle, which is not correct in Fig. 2. The hidden3d 1 option draws lines in the right order for a correctly looking 3d plot using line style 1. The additional set hidden3d command takes care of showing only those lines that are visible in 3d. These options will result in Fig. 3.

Fig. 3 Klein bottle plotted only with pm3d and hidden3d (code to produce this figure)

In order to reach at Fig. 1 we just have to set the surface to be transparent, which can be done by the set style fill command.

set style fill transparent solid 0.65

Tags: depthorder, hidden3d, parametric, pm3d, splot, transparent

Gnuplotting

Plotting raster data from Natural Earth

Plotting cubes

Interpolation of heat maps

Heat maps

Klein bottle

Gnuplot Links